Exercise 10.3.16

Proof.

(a)

Let $Q\in l_2$. Then $Q$ is obtained by verging with $P$ and $l_1,l_2$ if and only if there is a point $R\in l_1$ such that $\mathit{QR}=1$, if and only if $R$ is on the conchoid.

(b)

As $\mathit{QR}=1$, with $R$ on $l$, $Q$ is on the conchoid determined by $P$ and $l$, and on the unit circle, so $Q$ is at the intersection of the unit circle and the conchoid.

(c)

Here $P=(0,0)$ and $l$ is the horizontal line $y=-b,b>0$, in the Cartesian coordinates system $(P,{\stackrel{\to }{e}}_1,{\stackrel{\to }{e}}_2)$.

If $R$ is any point on $l$, then $\stackrel{\to }{\mathit{PR}}=\rho \stackrel{\to }{u}$, where

$$\stackrel{\to }{u}=\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃{\stackrel{\to }{e}}_1+\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃{\stackrel{\to }{e}}_2,𝜃\in ℝ\setminus \{\mathit{k\pi },k\in \mathbb{Z}\}.$$

The equation of the line $l_R=(\mathit{PR})$ is given for $M=(x,y)\in l_R$ by $\det <!--\; FUNCTION\; APPLICATION\; -->(\stackrel{\to }{\mathit{PM}},\stackrel{\to }{u})=0$:

$$x\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃-y\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃=0,$$

thus

$$R=\left(-b\frac{\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃},-b\right).$$

Let $𝒞$ be the conchoid, and let $(r,𝜃)$ the polar coordinates of a point $Q=(x,y)=(r\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃,r\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃)$ where $Q$ is a point in the line $\mathit{PR}$. Then

$$\stackrel{\to }{\mathit{PQ}}=r\stackrel{\to }{u}=r(\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃{\stackrel{\to }{e}}_1+\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃{\stackrel{\to }{e}}_2),$$

where $𝜃\in ℝ\setminus \{\mathit{k\pi },k\in \mathbb{Z}\}$, and $r\in ℝ$ may be positive or negative.

$$\begin{array}{llll}\hfill Q\in 𝒞& ⟺\mathit{QR}=1& \hfill & \\ \hfill & ⟺1={\left(x+b\frac{\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\right)}^2+{(y+b)}^2& \hfill & \\ \hfill & ⟺{\left(r\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃+b\frac{\cos <!--\; FUNCTION\; APPLICATION\; -->𝜃}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\right)}^2+{(r\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃+b)}^2=1& \hfill & \\ \hfill & ⟺{\left(r+\frac{b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\right)}^2=1& \hfill & \\ \hfill & ⟺r=\frac{-b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\pm 1(=-b\csc <!--\; FUNCTION\; APPLICATION\; -->𝜃\pm 1).& \hfill & \end{array}$$

So the polar equation of the conchoid of Nicomedes is

$$r=\frac{-b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\pm 1,𝜃\in ℝ\setminus \{\mathit{k\pi },k\in \mathbb{Z}\},$$

where the sign of $\pm 1$ gives the two portions of the curve.

$\mathit{PR}=\left|\frac{b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\right|$.

If $𝜃\in ]0,\pi [$, then $r<0$ and $-\frac{b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}<0$, so $\frac{-b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}-1$ give the portion below the line $l$, and $\frac{-b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}+1$ give the portion above.

If $𝜃\in ]-\pi ,0[$, then $r>0$ and $-\frac{b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}>0$, so $\frac{-b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}-1$ give the portion above the line $l$, and $\frac{-b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}+1$ give the portion below.

This is confirmed by the instruction "polar_plot" with Sage, where the blue and red portions of the conchoid are exchanged when $𝜃\in ]0,\pi [$ and $𝜃\in ]-\pi ,0[$ (see figure).

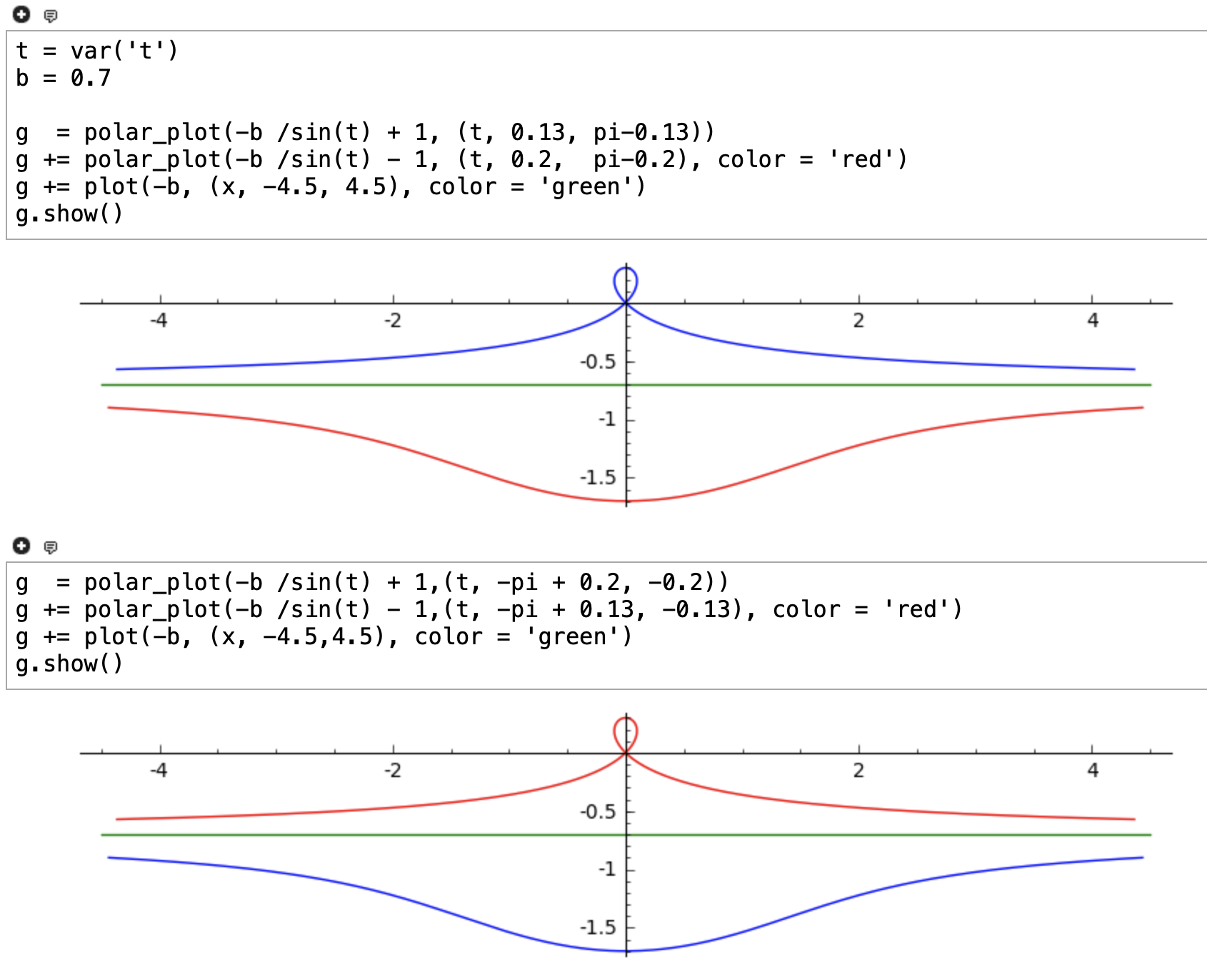
So, when $𝜃$ traces $ℝ$, the mobile point passes through the infinity point of the curve when $𝜃=\mathit{k\pi },k\in \mathbb{Z}$, and the two parts of the curve are traced with only one of the two formulas, for instance $r=-b\csc <!--\; FUNCTION\; APPLICATION\; -->𝜃+1$.

(d)

Any non horizontal line $l_1$ has an equation $x=\mathit{py}$, where $p=0$ or $p=1∕m$, $m$ being the slope of $l_1$. The intersection point $R$ of $l$ with $l_1$ is $R=(-\mathit{pb},-b)$, so, if $Q=(x,y)$, $$\begin{array}{llll}\hfill Q\in 𝒞& ⟺\exists <!--\; FUNCTION\; APPLICATION\; -->p\in ℝ,Q\in l_1\mathrm{and}\mathit{QR}=1& \hfill & \\ \hfill & ⟺\exists <!--\; FUNCTION\; APPLICATION\; -->p\in ℝ,\{\begin{array}{ccc}\hfill x\hfill & \hfill =\hfill & \mathit{py}\hfill \\ \hfill 1\hfill & \hfill =\hfill & {(x+\mathit{pb})}^2+{(y+b)}^2\hfill \end{array}& \hfill & \\ \hfill & ⟺(x,y)=(0,0)\mathrm{or}{\left(x+b\frac{x}{y}\right)}^2+{(y+b)}^2=1& \hfill & \\ \hfill & ⟺x^2{(y+b)}^2+y^2{(y+b)}^2=y^2& \hfill & \\ \hfill & ⟺(x^2+y^2){(y+b)}^2=y^2.& \hfill & \end{array}$$

(The polar equation gives the same Cartesian equation. For $r\ne 0$,

$$\begin{array}{llll}\hfill {\left(r+\frac{b}{\sin <!--\; FUNCTION\; APPLICATION\; -->𝜃}\right)}^2=1& ⟺{(y+b)}^2={\sin <!--\; FUNCTION\; APPLICATION\; -->}^2𝜃=\frac{y^2}{r^2}& \hfill & \\ \hfill & ⟺(x^2+y^2){(y+b)}^2=y^2.)& \hfill & \end{array}$$

The sign $\text{−}$ in the text seems to be a misprint, if the equation of $l$ is $y=-b$ (correct if the equation of $l$ is $y=b$).