Exercise 15.1.6

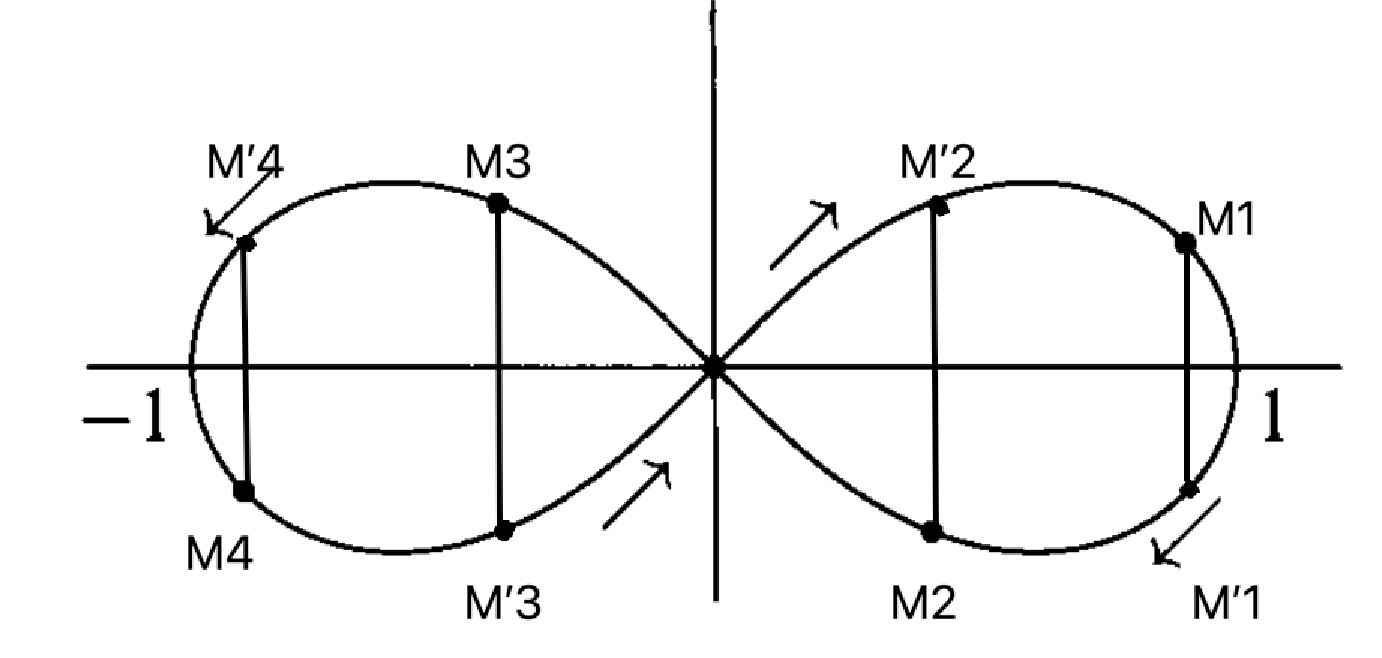
Proof. Suppose that $n=2N+1$ is odd, and consider $M_0=0,\dots ,M_{n-1}$ the $n$-divisions points, where $M_k$ has positive arc length $s_k=k\frac{2\varpi }{n},k=0,\dots ,n-1$.

Then $s_k=(2k)\frac{2\varpi }{2n}$, so that $N_{2k}=M_k$ is also a $2n$-division point. The other $2n$-division points are the points $N_{2k+1}$ corresponding to the arc length $k\frac{2\varpi }{n}+\frac{\varpi }{n}=(2k+1)\frac{\varpi }{n}$. Then the symmetric point $N_{2k+1}^{\prime }$ about the $x$-axis has arc length

thus is the $n$-division point $M_{2n+1-k}$. This proves that the symmetric points $M_0^{\prime }=0,\dots ,M_{n-1}^{\prime }$ of $M_0,\dots ,M_{n-1}$ about the $x$-axis are $2n$-divisions points.

Therefore we can complete $M_0,M_1,\dots ,M_{n-1}$ by the symmetric points $M_0^{\prime }=O,\dots ,M_{n-1}^{\prime }$ relative to the $x$-axis to obtain the $2n$-division points (the point $O$ is counted twice).

Since the $M_k$ can be constructed with straightedge and compass, the symmetric points $M_k^{\prime }$ are also constructible, thus the $2n$-division points are constructible.

Figure for $n=5$: the $10$-division points are $0,M_2^{\prime },M_1,M_1^{\prime },M_2,0,M_3,M_3^{\prime },M_4,M_3^{\prime }$.