Exercise 7.5.10

Proof.

(a)

Write $S$ the set of the 6 vertices of the octahedron, with coordinates $$(\pm 1,0,0),(0,\pm 1,0),(0,0,\pm 1),$$

and $G$ the group of rotations that carry $S$ to itself. $G$ acts transitively on $S$, we can go from a vertex to a near vertex by a rotation of angle $\pm \pi ∕2$, the axe being orthogonal to the plane containing these two summits and $O$. The orbit ${\mathcal{}O}_{\nu }$ of a fixed vertex $\nu$ is so the whole octahedron $S$:

$$|{\mathcal{}O}_{\nu }|=6.$$

Write $G_{\nu }$ the stabilizer in $G$ of the vertex $\nu$.

Every rotation $r\in G$ gives a permutation of the 6 vertices of the octahedron, thus fixes their gravity center $O=(0,0,0)$. If $r\in G_{\nu }\setminus \{e\}$, $r$ fixes $O$ and $\nu$, so is a rotation of axis $0\nu$. Thus, if $P$ is the orthogonal plane of the axe $0\nu$, $r$ sends $P$ on itself. The restriction of $r$ to this plane is so a rotation that carry the square of vertices of $S$ which lie in this plane to itself. So it is a rotation of angle $\mathit{k\pi }∕2,k=0,1,2,3$. As the rotation $r$ of axis $\mathit{O\nu }$ is uniquely determined by this restriction, $G_{\nu }$ is so the set of 4 rotations of axis $\mathit{O\nu }$, and of angle $\mathit{k\pi }∕2,k=0,1,2,3$.

$$|G_{\nu }|=4.$$

The Fundamental Theorem of Group Actions gives then $|O_{\nu }|=[G:G_{\nu }]$, thus

$$|G|=|O_{\nu }|\times |G_{\nu }|=6\times 4=24.$$

(b)

As a rotation $r\in G$ is an isometry, $r$ sends the 3 points of a face of the octahedron on the three points of a face of the same octahedron, so sends the gravity center of a face on the gravity center of the image. The cube $C$ whose vertices are the center of the faces of the octahedron is so invariant by $G$. Conversely if a rotation $r$ let invariant the cube $C$, it let invariant the octahedron whose vertices are the centers of the 6 faces of the cube de $S$, this octahedron is a dilatation of $S$, thus $r\in G$. So $G$ is the symmetry group of $C$.

(c)

As $r\in G$ is an isometry, $r$ sends a long diagonal on a long diagonal, and two distinct long diagonal have not the same image. $r$ gives then a permutation of the 4 diagonals, numbered 1,2,3,4, and so induces a permutation of $S_4$. The composition of two rotations corresponds to the composition of two permutations. So we obtain a group homomorphism $$\phi :G\to S_4.$$

(d)

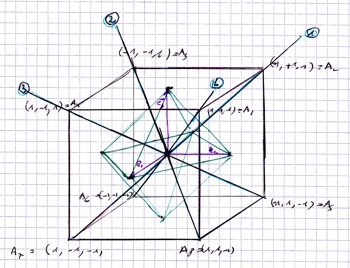
The cube of the centers of the faces of $S$ is a dilatation of a cube whose vertices are the points $(\pm 1,\pm 1,\pm 1)$,

$$\begin{array}{llll}\hfill & A_1=(1,1,1),A_2=(-1,1,1),A_3=(-1,-1,1),A_4=(1,-1,1),& \hfill & \\ \hfill & A_5=(-1,1,-1),A_6=(-1,-1,-1),A_7=(1,-1,-1),A_8=(1,1,-1).& \hfill & \end{array}$$

We give an arbitrary numbering of the four long diagonals:

$$\begin{array}{llll}\hfill D_1& =A_2{A}_7,D_2=A_3{A}_8,D_3=A_4{A}_5,D_4=A_1{A}_6.& \hfill & \end{array}$$

The rotation $r_1=\mathrm{Rot}(\pi ,\stackrel{\to }{e_1})$ exchanges $A_4$ and $A_8$, and also $A_2$ and $A_6$, thus exchanges $D_3$ with $D_2$, $D_1$ with $D_4$ :

$$\phi (r_1)=(14)(23).$$

$r_2=\mathrm{Rot}(\pi ∕2,\stackrel{\to }{e_3})$ gives the cycle $A_1\mapsto A_2\mapsto A_3\mapsto A_4\mapsto A_1$, thus $D_1\mapsto D_2\mapsto D_3\mapsto D_4\mapsto D_1$ :

$$\phi (r_2)=(1234).$$

$r_3=\mathrm{Rot}(\pi ∕2,\stackrel{\to }{e_2})$ gives $A_1\mapsto A_8\mapsto A_5\mapsto A_2\mapsto A_1$, thus $D_1\mapsto D_4\mapsto D_2\mapsto D_3\mapsto D_1$:

$$\phi (r_3)=(1423).$$

(e)

Let $H=⟨(14)(23),(1234),(1423)⟩\subset S_4$.

$H$ contains $[(14)(23)]\circ (1234)=(13)$. Moreover the two permutations $(13)=(31),(1423)=(3142)$ generate $S_4$, since $(a_1{a}_2),(a_1{a}_2\cdots a_n)$ generate $S_n$ generally. Thus $H=G$:

$$S_4=⟨\phi (r_1),\phi (r_2),\phi (r_3)⟩.$$

(f)

As the subgroup $\phi (G)$ contains $\phi (r_1),\phi (r_2),\phi (r_3)$, it contains $S_4=⟨\phi (r_1),\phi (r_2),\phi (r_3)⟩$. Therefore $$\phi (G)=S_4.$$

So $\phi :G\to S_4$ is surjective. Moreover $|G|=|S_4|=24$, so $\phi$ is bijective, $\phi :G\to S_4$ is thus an isomorphism.

$$G\simeq S_4.$$

As $\phi (G)=⟨\phi (r_1),\phi (r_2),\phi (r_3)⟩$, where $\phi$ is an isomorphism,

$$G=⟨r_1,r_2,r_3⟩.$$