Exercise 1.11 (Optimal currency conversion)

Question

Suppose that there are $N$ available currencies, and assume that one unit of currency $i$ can be exchanged for $r_{i j}$ units of currency $j$. (Naturally, we assume that $r_{i j}>0$.) There also certain regulations that impose a limit $u_{i}$ on the total amount of currency $i$ that can be exchanged on any given day. Suppose that we start with $B$ units of currency 1 and that we would like to maximize the number of units of currency $N$ that we end up with at the end of the day, through a sequence of currency transactions. Provide a linear programming formulation of this problem. Assume that for any sequence $i_{1}, \ldots, i_{k}$ of currencies, we have $r_{i_{1} i_{2}} r_{i_{2} i_{3}} \cdots r_{i_{k-1} i_{k}} r_{i_{k} i_{1}} \leq 1$, which means that wealth cannot be multiplied by going through a cycle of currencies.

Elu Thingol · Accepted Answer

We model the amount of currencies exchanged from the currency $i$, $i=1,\ldots,N$ for a currency $j$, $j=1,\ldots,12$, by $x_{ij}$. Our goal is to maximize the amount of currency in $N$

$$\sum_{j=1}^{N} r_{jN} \cdot x_{jN}$$

under the condition that current regulations impose a limit $u_i$ on the total amount of currency $i$ that can be exchanged on any given day:

$$\sum_{j=1}^{N} x_{ij} \leq u_i, \quad i=1,\ldots,N,$$

and that we have a starting amount of $B$ currency $i$:

$$\sum_{j=1}^{N} x_{1j} \leq B.$$

Obviously, we cannot exchange more currency from $i$ to other currencies than we changed to $i$ before:

$$\sum_{j=1}^{N} r_{ji}x_{ji} \geq \sum_{k=1}^{N} x_{jk}, \quad i=2,\ldots,N.$$

and no currency will be exchanged for currency 1 or from currency N:

$$x_{i1} = 0, \quad x_{Ni} = 0, \quad i=1,\ldots,N.$$

\begin{figure}
\includegraphics[width=1	extwidth]{bertsimas_linopt_exercise_1-11.png}
\caption{Conversion possibilities for the currencies.}
\end{figure}

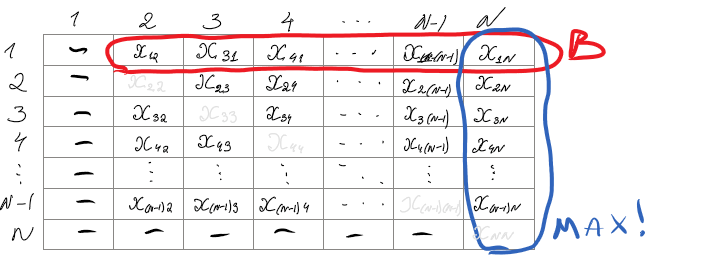
These conditions result in the following linear optimization problem:

\begin{equation*}
\begin{array}{llll}
	ext{maximize} \quad &\sum_{j=1}^{N} r_{jN} \cdot x_{jN}\
	ext{subject to} \quad
&\sum_{j=1}^{N} x_{ij} \leq u_i, \quad &i=1,\ldots,N\
&\sum_{j=1}^{N} x_{1j} \leq B\
&\sum_{j=1}^{N} r_{ji}x_{ji} \geq \sum_{k=1}^{N} x_{jk}, \quad &i=2,\ldots,N\
&x_{i1} = 0, \quad x_{Ni} = 0, \quad &i=1,\ldots,N\
&x_{ij} \geq 0, \quad &i=1,\ldots,N, &j=1,\ldots,N
\end{array}
\end{equation*}

Exercise 1.11 (Optimal currency conversion)

Answers

Comments

Exercise 1.11 (Optimal currency conversion)

Answers

Comments

Add answer