Exercise 1.14

Question

A company produces and sells two different products. The de­mand for each product is unlimited, but the company is constrained by cash availability and machine capacity.\par 

Each unit of the first and second product requires 3 and 4 machine hours, respectively. There are 20,000 machine hours available in the current production period. The production costs are \$3 and \$2 per unit of the first and second product, respectively. The selling prices of the first and second product are \$6 and \$5.40 per unit, respectively. The available cash is \$4,000; furthermore, 45\% of the sales revenues from the first product and 30\% of the sales revenues from the second product will be made available to finance operations during the current period.
\begin{enumerate}[label=(\alph*)]
\item Formulate a linear programming problem that aims at maximizing net in­ come subject to the cash availability and machine capacity limitations.
\item Solve the problem graphically to obtain an optimal solution.
\item Suppose that the company could increase its available machine hours by 2,000, after spending \$400 for certain repairs. Should the investment be made?
\end{enumerate}

Elu Thingol · Accepted Answer

\begin{enumerate}[label=(\alph*)]
\item We denote the number of units of the first product by $x$ and the number of units of the second product by $y$; both are nonnegative real numbers. Our goal is to maximize the profit (not revenue) function given by

$$(1-0.45)\cdot 6x + (1-0.30)\cdot 5.40y = 3.3x + 3.78 y.$$

under the condition that the total machine hours capacity does not exceed twenty thousand hours

$$3x + 4y \leq 20,000$$

and 45\% of the revenues for the first product as well as the 30\% of the sales revenues from the second product plus the fixed amount of $\$4,000$ are available for operations

$$3x + 2y \leq 4000 + 0.45 \cdot 6x + 0.3 \cdot 5.4.$$

This results in the following linear optimization problem:

\begin{equation}
\begin{array}{ll}
\operatorname{maximize}\quad &3.3x + 3.78 y \
	ext { subject to}\quad & 3x + 4y \leq 20000 \
&0.3x + 0.38y \leq 4000\
&x,y \geq 0.
\end{array}
\end{equation}

\item Since all quantities are nonnegative, we only work in the first quadrant. The first constraint is the area below the function $y = 5,000-\frac{3}{4}x$, the second constraint is the area below the function $y = \frac{4,000 - 0.3x}{0.38}$. The feasible region is then the intersection of both areas. Classes of $[x,y]$ characterised by the same profit are marked via red lines $y = \frac{z - 3.3x}{3.78}$, where $z$ is the corresponding net income (they are the isolines of the three-dimensional graph $f(x,y) = 3.3x + 3.78 y$ which is monotonically increasing with both $x$ and $y$). In the figure below, the feasible region is dark green, whereas the objective function isolines are marked red.

\begin{figure}
\includegraphics[width=0.9	extwidth]{bertsimas_linopt_exercise_1-14_1.png}
\end{figure}

As we can see, the second constraint ($0.3x + 0.38y \leq 4000$) is redundant and will not be considered from here on. The optimal cost (highest isoline touching the feasible region) emerges from the corner solution $\begin{bmatrix} 20,000/0.3 \ 0 \end{bmatrix}$. This results in the optimal profit of $\$20,000$.

\item The new constraint is $3x + 4y \leq 22000$. Modifying our sketch (the old constraint is dark green, the new constraint is light green), we obtain:

\begin{figure}
\includegraphics[width=0.9	extwidth]{bertsimas_linopt_exercise_1-14_2.png}
\end{figure}

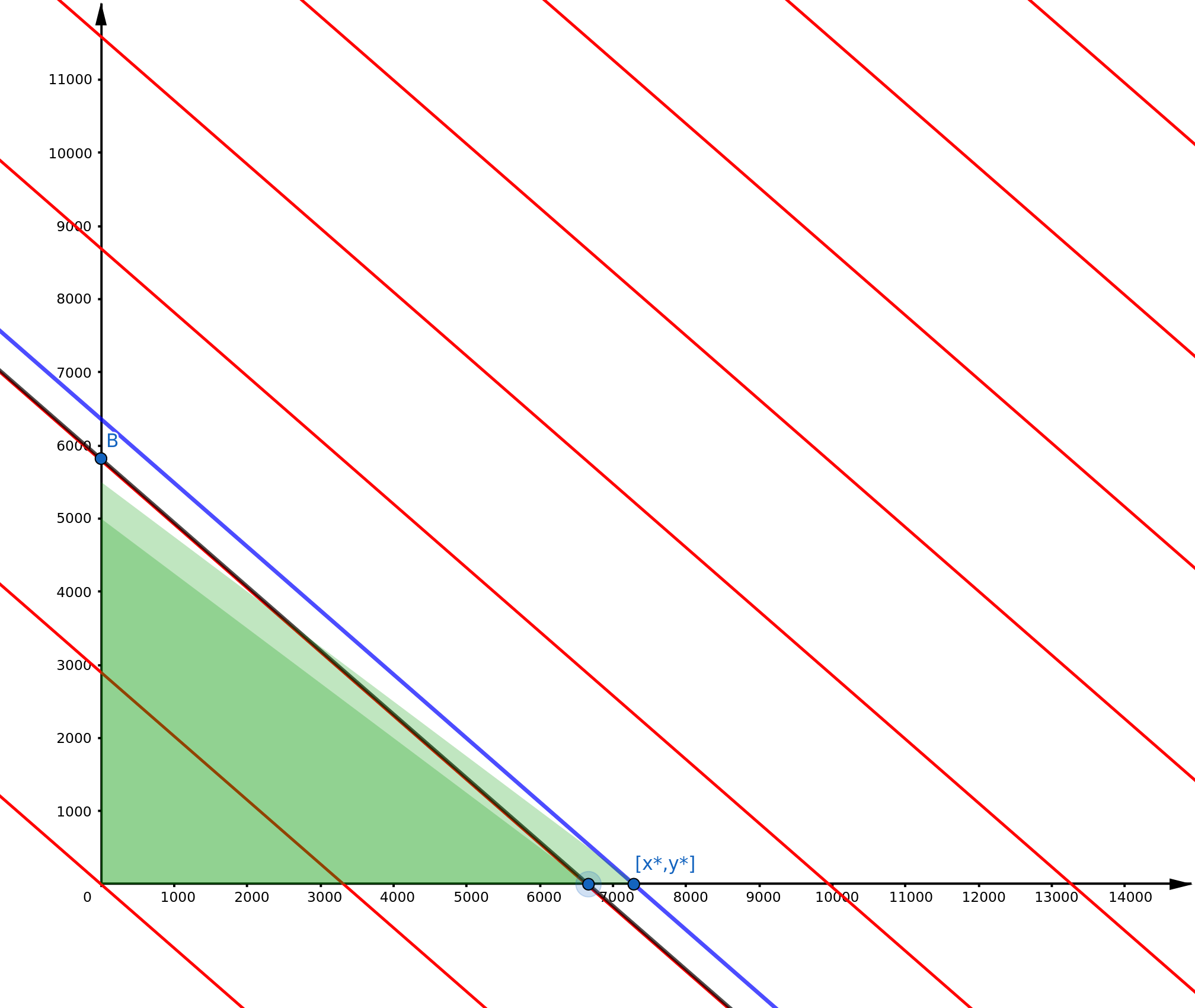
The optimal solution has now shifted to the point $\begin{bmatrix} 22000/3 \ 0 \end{bmatrix}$, resulting in the optimal net income of $\$24,200$. The increase in profit is thus $\$24,200 - \$22,000 = \$2,200$, which exceeds the costs associated with the investment. Thus, the company should invest in machine reparations.

\end{enumerate}

Exercise 1.14

Answers

Comments

Exercise 1.14

Answers

Comments

Add answer