Exercise 2.10

Question

Consider the standard form polyhedron $\left\{\mathbf{x} \mid \mathbf{A}\mathbf{x} = \mathbf{b},\, \mathbf{x}\geq \mathbf{0}ight\}$. Suppose that the matrix $\mathbf{A}$ has dimensions $m	imes n$ and that its rows are linearly independent. For each of the following statements, state whether it is true of false. If true, provide a proof, else, provide a counterexample.
\begin{enumerate}[label=(\alph*)]
\item If $n = m + 1$, then $P$ has at most two basic feasible solutions.
\item The set of all optimal solutions is bounded.
\item At every optimal solution, no more than m variables can be positive.
\item If there is more than one optimal solution, then there are uncountably many optimal
solutions.
\item If there are several optimal solutions, then there exist at least two basic feasible solutions
that are optimal.
\item Consider the problem of minimizing $\max\{\mathbf{c'x}, \mathbf{d'x}\}$ over the set $P$. If this problem has an optimal solution, it must have an optimal solution which is an extreme point of $P$.
\end{enumerate}

Elu Thingol · Accepted Answer

\defank{	ext{rank}}
\def
ull{	ext{null}}
(a) This assertion is true. The geometric intuition behind this assertion is that $P$ is a polyhedron in $\mathfrak{R}^{m+1}$ that is contained in a subset of the intersection of $m$ hyperplanes
$$P \subseteq \bigcap_{i=1}^{m} \left\{ \mathbf{x} \in \mathfrak{R}^n \mid \mathbf{a}'_i \mathbf{x} = b_iight\}.$$
Recall that an intersection of $m$ (linearly independent) hyperplanes in an $m+1$ dimensional space always results in a line. As a convex subset of this line, polyhedron $P$ must either be a line itself, or a ray, or a line segment. In any of these cases, the resulting figure has at most two extreme points. We now formalize this argument.
\begin{proof}
We first demonstrate that $P$ is a convex subset of some line. Since $\mathbf{A}$ has $ank(\mathbf{A})=m$, by \href{https://en.wikipedia.org/wiki/Rank-nullity_theorem}{rank-nullity theorem} we conclude that the null space $
ull(\mathbf{A})$ of $\mathbf{A}$ is a one-dimensional vector subspace of $\mathfrak{R}^{m+1}$, i.e., a line. But then the null space of the affine mapping $\mathbf{A}\mathbf{x}-\mathbf{b}$ must be a line as well. To see why, let $\mathbf{x}^* \in P$ be a vertex of $P$. Then,
$$P \subseteq 
ull(A) + \mathbf{x}^*.$$
[If $\mathbf{y}^* \in P$, then $\mathbf{y}^* = (\mathbf{x}^* - \mathbf{y}^*) + \mathbf{x}$ for $\mathbf{x}^* - \mathbf{y}^* \in 
ull(\mathbf{A})$.]
ewline
Now we demonstrate that a convex subset of a line can have at most $2$ extreme points. Suppose for the sake of contradiction that we can find three distinct extreme points $\mathbf{x}^*_1,\mathbf{x}^*_2,\mathbf{x}^*_3$ of $P$. By definition of a line, there exist scalars $\lambda_1,\lambda_2,\lambda_3 \in \mathfrak{R}$ and a vector $\mathbf{a}\in 
ull(A) + \mathbf{x}^*$ such that $\mathbf{x}_i = \lambda_i \mathbf{a}$. Since they all reside on the line, one of them must be between the two others; without loss of generality, assume that $\lambda_1 < \lambda_2 < \lambda_3$ and as such
$$\mathbf{x}^*_1 < \mathbf{x}^*_2 < \mathbf{x}^*_3.$$
Since $\mathbf{x}^*_2$ is between the two other solutions and $P$ is convex, we can write $\mathbf{x}^*_2$ as a convex combination of $\mathbf{x}^*_1$ and $\mathbf{x}^*_3$:
$$\frac{\lambda_2}{2\lambda_1}\mathbf{x}^*_1 + \frac{\lambda_2}{2\lambda_3}\mathbf{x}^*_3 = \mathbf{x}^*_2.$$
Hence, $\mathbf{x}^*_3$ cannot be an extreme point - a contradiction.
\end{proof}

Jannik Friese · Answer

(a) True. In fact $P$ is a polyhedron in $\mathfrak{R}^{m+1}$ that is contained in the intersection of $m$ hyperplanes. Since the $m$ rows of $A$ are linearly independent we get that $P$ is contained in a subspace of dimension $1$, therefore a line. Hence $P$ has at most two extreme points,
equivalently $P$ has at most two basic feasible solutions.\par

(b) False. Consider the polyhedron $P = \{\mathbf{x}\in\mathfrak{R}^2 \mid -x_1+2x_2=1, \mathbf{x}\geq\mathbf{0}\}$. Here $\mathbf{A}=\begin{bmatrix} -1 & 2\end{bmatrix}$ and $\mathbf{b} = \begin{bmatrix} 1 \end{bmatrix}$. 
\begin{figure}
\includegraphics[width=0.4	extwidth]{bertsimas_linopt_exercise_2-10_b.png}
\end{figure}
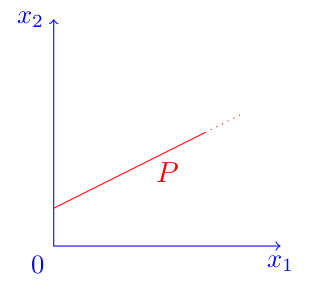
Suppose we are minimizing $\mathbf{c}'\mathbf{x}$, with $\mathbf{c}=\begin{bmatrix} -1 & 2\end{bmatrix}$. Then every point of $P$ is an optimal solution. Since $P$ is unbounded, also the set of optimal solutions is unbounded.\par

(c) False. Consider the following example where $P = \{\mathbf{x}\in\mathfrak{R}^2 \mid x_1+x_2=1, \mathbf{x}\geq\mathbf{0}\}$. Then $\mathbf{A}=\begin{bmatrix} 1 & 1\end{bmatrix}$ and $\mathbf{b} = \begin{bmatrix} 1 \end{bmatrix}$. The polyhedron $P$ is the red segment displayed below.
\begin{figure}
\includegraphics[width=0.4	extwidth]{bertsimas_linopt_exercise_2-10_c.png}
\end{figure}
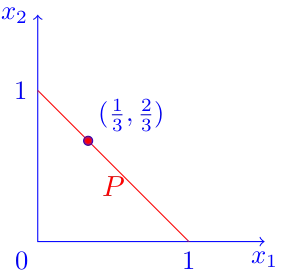
Assume that the objective function to minimize is $\mathbf{c}^{\prime} \mathbf{x}$ where $\mathbf{c}=\begin{bmatrix}1 \ 1\end{bmatrix}.$ In this case $m=1$ and every point in $P$ is an optimal solution. For example $\begin{bmatrix}\frac{1}{3}, \frac{2}{3}\end{bmatrix}$ is an optimal solution with more than $m$ positive variables.\par

(d) True. In fact, if we have two optimal solutions, every convex combination of those is an optimal solution too.
ewline
\begin{proof}
Suppose we want to minimize $\mathbf{c}^{\prime} x$ and let $\mathbf{x}_{1}, \mathbf{x}_{2}$ be two optimal solutions. It means that
$$\mathbf{c}^{\prime} \mathbf{x}_{1}=\mathbf{c}^{\prime} \mathbf{x}_{2}=\mathbf{c}^{*},$$
where $\mathbf{c}^{*}$ is the optimal objective value and $\mathbf{c}^{\prime} \mathbf{x} \geq \mathbf{c}^{*}$ for all $\mathbf{x} \in P$. Let $\lambda \in[0,1]$ and consider $\bar{\mathbf{x}}=\lambda \mathbf{x}_{1}+(1-\lambda) \mathbf{x}_{2}$. We want to show that $\bar{\mathbf{x}}$ is an optimal solution too. We have that
$$
\mathbf{c}^{\prime} \bar{\mathbf{x}}=\mathbf{c}^{\prime}\left(\lambda \mathbf{x}_{1}+(1-\lambda) \mathbf{x}_{2}ight)=\lambda \mathbf{c}^{\prime} \mathbf{x}_{1}+(1-\lambda) \mathbf{c}^{\prime} \mathbf{x}_{2}=\lambda \mathbf{c}^{*}+(1-\lambda) \mathbf{c}^{*}=\mathbf{c}^{*}
$$
therefore $\bar{\mathbf{x}}$ is an optimal solution.
\end{proof}\par

(e) False. The same counterexample of point (b) holds, in fact, there is only one basic feasible solution which is $\left(0, \frac{1}{2}ight)$. It is optimal because $P$ coincide with the set of optimal solutions.\par

(f) False. Let $P = \{\mathbf{x}\in\mathfrak{R}^2 \mid x_1+x_2=1, \mathbf{x}\geq\mathbf{0}\}$, let $\mathbf{c}=\begin{bmatrix}1 \ -1\end{bmatrix}$ and $\mathbf{d}=\begin{bmatrix}-1 \ 1\end{bmatrix}$.
ewline
So in this example we are minimizing on $P$ the $\max\{\mathbf{c'x}, \mathbf{d'x}\}=\max \left\{x_{1}-x_{2},-x_{1}+x_{2}ight\}$. The polyhedron $P$ is the segment joining the points $(0,1),(1,0)$ in red. The teal line represents the line in which $\max \left\{\mathbf c^{\prime} \mathbf x, \mathbf d^{\prime} \mathbf xight\}=0$. In fact above it we have $x_{2}>x_{1}$ and therefore $\max \left\{\mathbf c^{\prime} \mathbf x, \mathbf d^{\prime} \mathbf xight\}=\mathbf d^{\prime} \mathbf x>0$, below it $x_{1}>x_{2}$ and $\max \left\{\mathbf c^{\prime} \mathbf x, \mathbf d^{\prime} \mathbf xight\}=\mathbf c^{\prime} \mathbf x>0$.
\begin{figure}
\includegraphics[width=0.4	extwidth]{bertsimas_linopt_exercise_2-10_f.png}
\end{figure}
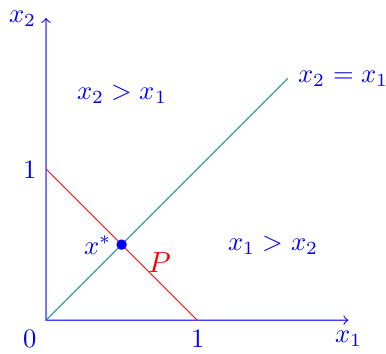
Hence $\min_{\mathbf{x}\in p}\max\{\mathbf{c'x}, \mathbf{d'x}\} = 0$ is achieved by $\mathbf{x}^* = \begin{bmatrix} \frac12 & \frac12 \end{bmatrix}'$.

Prakash Anand · Answer

(a) No, it is not true. Consider the standard form polyhedron $\{(x, y, z) \in$ $\left.\mathbb{R}^{3} \mid x+y=2, y+z=1 \quad x, y, z \geq 0\right\} .$ There are 3 basic solutions $(2,0,1),(0,2,-1),(1,1,0)$.\par

(b) No, it is not true. Consider the LP problem that minimize $-x+y$ over the standard form polyhedron $\left\{(x, y) \in \mathbb{R}^{2} \mid-x+y=0, \quad x, y \geq 0\right\}$. Then every point in the polyhedron is an optimal solution, and clearly, the polyhedron is not bounded.\par

(c) No, it is not true. Consider again the LP problem in (b). Then $(1,1)$ is an optimal solution with more than 1 positive variables.\par

(d) Yes, it is true. Let $x, y$ be two distinct optimal solutions and $d$ be the corresponding optimal value. Consider the convex combination of $x, y: \lambda x+(1-\lambda) y, \lambda \in[0,1]$. For all $\lambda \in[0,1], c^{\prime}[\lambda x+(1-\lambda) y]=\lambda d+(1-\lambda) d=d$. Also, since the polyhedron is a convex set, every convex combination of $x, y$ is in the polyhedron. Thus, we have uncountably many optimal solutions $\lambda x+(1-\lambda) y, \lambda \in[0,1]$.\par

(e) No, it is not true. Consider again the counterexample in (b). The polyhedron has only one basic feasible solution but infinitely many optimal solutions.\par

(f) Yes, it is true. Introduce new variables $z, s_{1}, s_{2} \in \mathbb{R}$ with constraints $c^{\prime} x+s_{1}=$ $z, d^{\prime} x+s_{2}=z$, and $z, s_{1}, s_{2} \geq 0 .$ Then we transform the LP problem into minimizing $z$ over a standard form polyhedron $P^{\prime}=\left\{\left(x_{1}, \ldots, x_{n}, z, s_{1}, s_{2}\right) \in \mathbb{R}^{n+3} \mid A x=\right.$ $\left.b, c^{\prime} x+s_{1}-z=0, d^{\prime} x+s_{2}-z=0, x, z, s_{1}, s_{2} \geq 0\right\}$ where $x=\left(x_{1}, \ldots, x_{n}\right) .$ Note that there are $n+3$ variables and $m+2$ equality constraints. Let $A^{\prime}$ be the $m+2$ by $n+3$ matrix of all equality constraints of $P^{\prime}$. Since the matrix $A$ has linearly independent rows and the new constraints $c^{\prime} x+s_{1}-z=0, d^{\prime} x+s_{2}-z=0$ involve new variables respectively, the matrix $A^{\prime}$ also has linearly independent rows. The LP problem has an optimal solution, so there is an extreme point $x^{\prime}=\left(x_{1}^{\prime}, \ldots, x_{n}^{\prime}, z^{\prime}, s_{1}^{\prime}, s_{2}^{\prime}\right)$ of $P^{\prime}$ that is an optimal solution. We now claim $x^{*}=\left(x_{1}^{\prime}, \ldots, x_{n}^{\prime}\right) \in \mathbb{R}^{n}$ is an optimal solution which is an extreme point of $P .$ Obviously, $x^{*} \in P .$ Note that $A_{(n+1)}^{\prime}+A_{(n+2)}^{\prime}=A_{(n+3)}^{\prime}$, so we can choose at most 2 linearly independent columns from $A_{(n+1)}^{\prime}, A_{(n+2)}^{\prime}, A_{(n+3)}^{\prime}$ when constructing a basic solution. That said, we have to choose at least $m$ columns from the first $n$ columns of $A$. However, we can choose at most $m$ linearly independent columns from the first $n$ columns because $\operatorname{rank}(A)=m$. Therefore, every extreme point of $P^{\prime}$ has a corresponding basis consisting $m$ vectors from the first $n$ columns of $A^{\prime} .$ This means $x^{*}$ has a corresponding basis consisting exactly $m$ vectors from the columns of $A$. Thus, $x^{*}$ is an extreme point of $P$ and clearly it is also an optimal solution to the LP problem.

Exercise 2.10

Answers

Comments

Comments

Comments

Exercise 2.10

Answers

Comments

Comments

Comments

Add answer