Exercise 3.1 (Local minima of convex functions)

Question

Let $f: \Re^{n} \mapsto \Re$ be a convex function and let $S \subset \Re^{n}$ be a convex set. Let $\mathbf{x}^{*}$ be an element of $S$. Suppose that $\mathbf{x}^{*}$ is a local optimum for the problem of minimizing $f(\mathbf{x})$ over $S$; that is, there exists some $\epsilon>0$ such that $f\left(\mathbf{x}^{*}\right) \leq f(\mathbf{x})$ for all $\mathbf{x} \in S$ for which $\left\|\mathbf{x}-\mathbf{x}^{*}\right\| \leq \epsilon$. Prove that $\mathbf{x}^{*}$ is globally optimal; that is, $f\left(\mathbf{x}^{*}\right) \leq f(\mathbf{x})$ for all $\mathrm{x} \in S$.

Elu Thingol · Accepted Answer

\begin{proof}
Let $\mathbf{x}^* \in S$ be a local minimum for $f$, i.e., there is an $\varepsilon > 0$ such that whenever $\|\mathbf{x} - \mathbf{x}^*\| \leq \varepsilon$, we have $f\left(\mathbf{x}^*ight) \leq f\left(\mathbf{x}ight)$. Suppose for the sake of contradiction that $\mathbf{x}^*$ is not a global minimum, i.e., there exists another element $\mathbf{y}^* \in S$ such that $f\left(\mathbf{y}^*ight) < f\left(\mathbf{x}^*ight)$. Consider the line segment between $\mathbf{x}^*$ and $\mathbf{y}^*$:

$$\left\{ \lambda \mathbf{x}^* + (1-\lambda) \mathbf{y}^* \mid \lambda \in [0,1]ight\}.$$

\begin{figure}
\includegraphics[width=0.75	extwidth]{bertsimas_linopt_exercise_3-1.png}
\caption{Strategy to construct a contradiction.}
\end{figure}

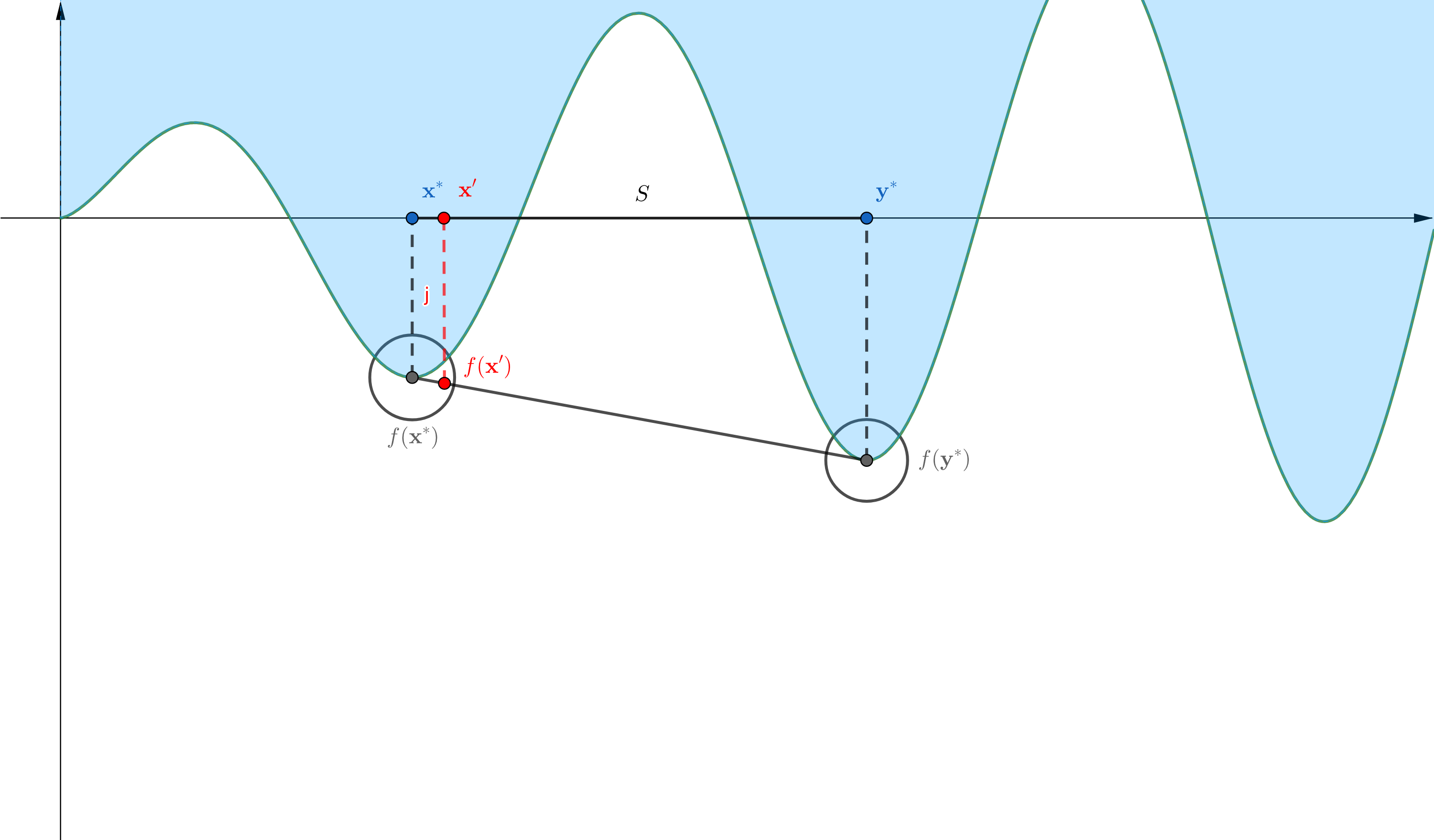
This line is entirely contained in $S$ by the convexity assumption. Furthermore, the elements of this line can get arbitrarily close to $\mathbf{x}^*$:

\begin{align*}
\| \mathbf{x}^* -  \lambda \mathbf{x}^* + (1-\lambda) \mathbf{y}^* \| &\leq \varepsilon \
(1-\lambda) \|\mathbf{x}^* + \mathbf{y}^*\| &\leq \varepsilon \
\lambda &\approx 1.
\end{align*}

But the resulting combination creates a weighted average of $f\left(\mathbf{x}^*ight)$ and $f\left(\mathbf{y}^*ight)$ which is obviously less that $f\left(\mathbf{x}^*ight)$ alone:

$$f\left( \lambda \mathbf{x}^* + (1-\lambda) \mathbf{y}^* ight)
\leq \lambda f\left(\mathbf{x}^*ight) + (1-\lambda) f\left(\mathbf{y}^*ight) 
< \lambda f\left(\mathbf{x}^*ight) + (1-\lambda) f\left(\mathbf{x}^*ight) 
= f\left(\mathbf{x}^*ight).
$$

In other words, we have found a point $\mathbf{x}' = \lambda \mathbf{x}^* + (1-\lambda) \mathbf{y}^*$ in the $\varepsilon$-neighbourhood of $\mathbf{x}$ such that $f\left(\mathbf{x}'ight) < f\left(\mathbf{x}^*ight)$. This is a contradiction to the fact that $f\left(\mathbf{x}^*ight)$ is a local minimum in its $\varepsilon$-neighbourhood.

\end{proof}

Exercise 3.1 (Local minima of convex functions)

Answers

Comments

Exercise 3.1 (Local minima of convex functions)

Answers

Comments

Add answer