Homepage › Solution manuals › Ivan Niven › An Introduction to the Theory of Numbers › Exercise 5.6.10 (Finite subgroup of an elliptic curve)
Exercise 5.6.10 (Finite subgroup of an elliptic curve)
Show that the cubic curve is nonsingular. Note that this curve contains the four rational points . Apply the chord-and-tangent method to these points and note the results.
Answers
Proof.
- (a)
-
Put
and
.
We show that the cubic curve is nonsingular. Since for all
in singular iff and only if and , that is if . But , thus has no solution.
(To prove that is an elliptic curve, we must also verify that the point at infinity of the curve is non singular.)
- (b)
-
contains the rational points
. There is also
, the unique point of intersection of
with the
-axis.
The homogeneous equation of is . We obtain the points at infinity with , thus . The unique point at infinity of the curve is
We write the third point of intersection of two points of the curve, and the symmetric point of relative to the -axis. In section 5.7, the authors prove that the set of rational points of the elliptic curve is a group for this law , with the point at infinity as neutral element. The opposite of is the symmetric of relative to the -axis, so that , (and ).
Starting from , we compute , , and so on.
-
The tangent at point has for equation
thus the equation of is . Since , and .
-
The chord has for equation , thus , so
-
Since the tangent line at is vertical, , that is , so that
The point has order 6, and , . Therefore, the group generated by is
which contains the initial points . So the chord-and-tangent method starting of these points is achieved.
is a subgroup of , isomorphic to .
-
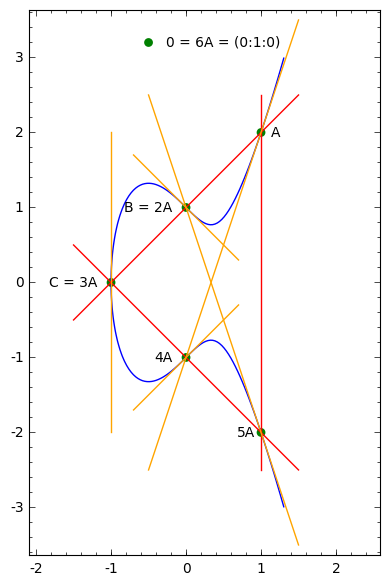
Note: Since , and . This means that (and ) are inflection points of the curve (see figure).
