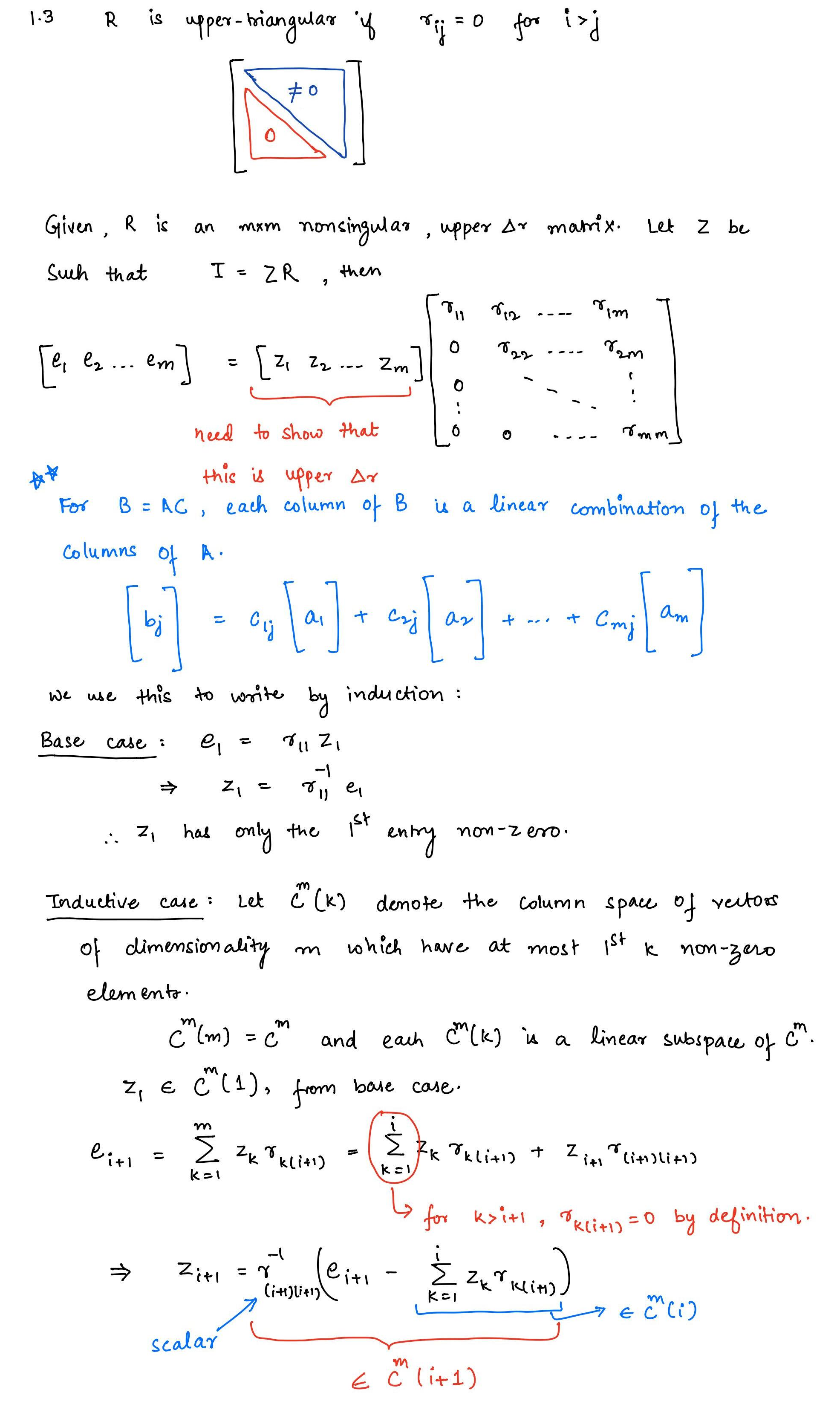Exercise 1.3

Generalizing Example 1.3, we say that a square or rectangular matrix $R$ with entries $r_{\mathit{ij}}$; is upper-triangular if $r_{\mathit{ij}}=0$ for $i>j$. By considering what space is spanned by the first $n$ columns of $R$ and using (1.8), show that if $R$ is a nonsingular $m\times m$ upper-triangular matrix, then $R^{-1}$ is also upper-triangular. (The analogous result also holds for lower-triangular matrices.)