Exercise 1.6.23 (Cousin's theorem)

Question

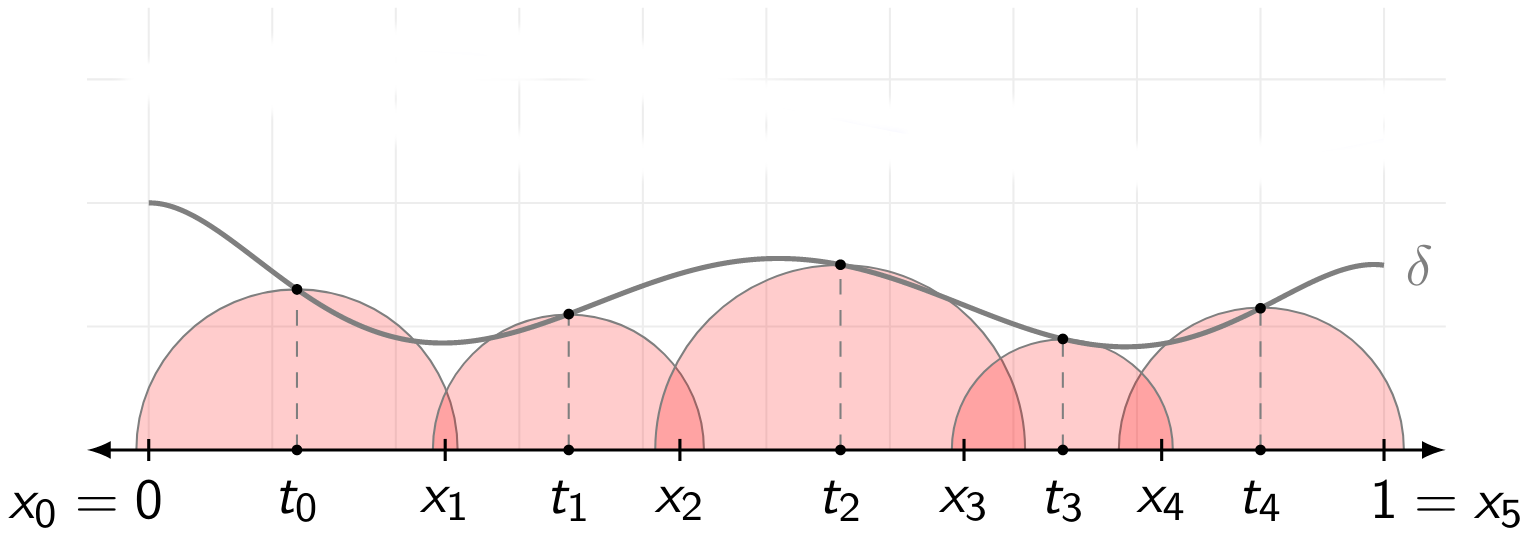
Prove Cousin’s theorem: given any function $\delta: [a,b] \rightarrow (0,+\infty)$ on a compact interval $[a,b]$ of positive length, there exists a partition $a = t_0 < t_1 < \ldots < t_k = b$ with $k \geq 1$, together with real numbers $t^*_j \in [t_{j-1},t_j]$ for each $1 \leq j \leq k$ and $t_j - t_{j-1} \leq \delta(t^*_j)$.

Elu Thingol · Accepted Answer

\begin{proof}
To construct a partition for Cousin's theorem\footnote{This result was originally proved by Pierre Cousin, a student of Henri Poincaré, in 1895. Thus, the naming has nothing to do with any kind of relatives or relationships in general.}, we implement the following algorithm.
\begin{lstlisting}[language=python]
c = b - a
t = δ⁻¹([c,∞))
while (t ≠ Ø):
   c = c / 2
   t = δ⁻¹([c,∞))
partition = {[a+i*c,a+(i+1)*c] for i=0,...,(b-a)/c}
\end{lstlisting}
Heuristically, the algorithm suggests starting with the largest possible value of $\delta$ that is allowed for this partition: $b-a$. If the gauge function $\delta$ never exceeds this value, then we already have our partition $\langle a, b angle$ where the middle point $t^*$ can be any point between $a$ and $b$. If, however, $\delta$ does exceed $b-a$ somewhere, then we must search further. Splitting $[a,b]$ in half, we check whether $\delta$ exceeds $\frac{b-a}{2}$ on both halves of $[a,b]$. If this is not the case, then we are done as we have a partition $\langle a, \frac{b+a}{2}, b angle$ with the middle points $t^*_1,t^*_2$ anywhere in between. If that is not the case, we further split the interval into four parts and repeat the procedure with $\frac{b-a}{4}$.

\begin{figure}
\includegraphics[width=0.5	extwidth]{tao_measure_exercise_1-6-23_gauge-algorithm.png}
\caption{Algorithm for constructing a gauge partition on $[0,1]$. Red intervals are the accepted subintervals whereas the black ones are the ones that initiate the further search.}
\end{figure}

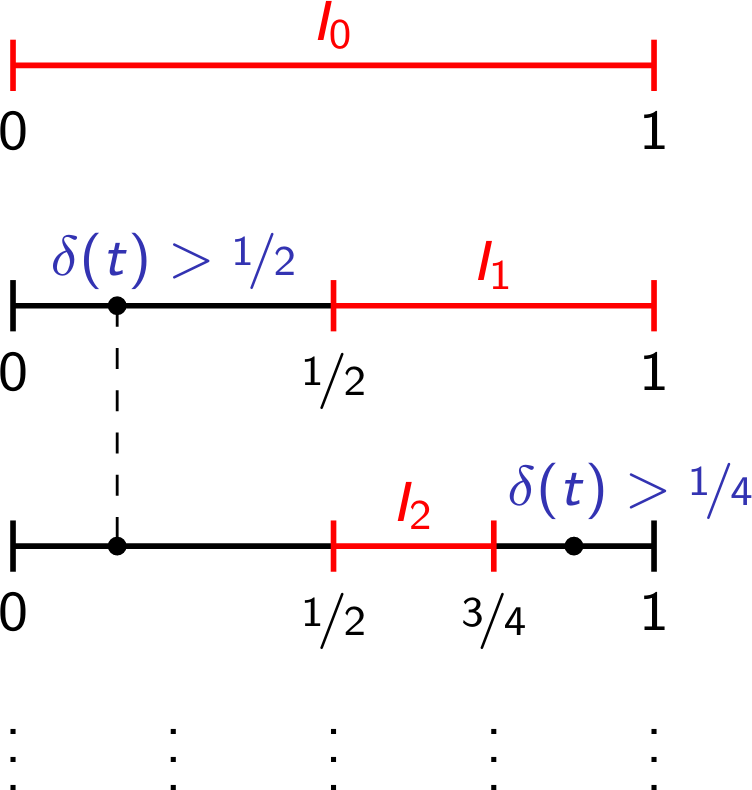
The above algorithm is guaranteed to terminate. If that would not be the case, then we could find a $x \in \bigcap_{n=1}^{\infty} I_n$ such that for all $n\in\mathbb{N}$ we would have $\delta(x^*) < \frac{b-a}{n}$, i.e., $\delta(x^*) = 0$ - a contradiction to the positivity assumption on $\delta$.

\begin{figure}
\includegraphics[width=	extwidth]{tao_measure_exercise_1-6-23_gauge.png}
\caption{A gauge partition on $[0,1]$ (by Jordan Barrett).}
\end{figure}
\end{proof}

Exercise 1.6.23 (Cousin's theorem)

Answers

Comments

Exercise 1.6.23 (Cousin's theorem)

Answers

Comments

Add answer