Exercise 1.7.18 (Product $\sigma$-algebras)

Recall that to show that two families of sets generate the same $\sigma$-algebra, it suffices to show that every $\sigma$-algebra that contains the former family of sets, contains the latter also, and conversely.

• Pick an arbitrary $A$ from the generating set of the product $\sigma$-algebra. Then either $A={\pi }_X^{-1}(E)$ for some $E\in B_X$ or $A={\pi }_Y^{-1}(F)$ for some $F\in B_X$. In the former case, it is obvious that $A=E\times Y$. But both $E\in B_X$ and $Y\in B_Y$; thus, $A$ must be contained in the generating set on the right-hand side. The second case follows identically.
• Pick an arbitrary $E\times F$ for some $E\in B_X$ and $F\in B_Y$. Then, it is easy to verify that $E\times F=(X\times F)\cap (E\times Y)$. The former $X\times F$ is the pullback of the set $F$ under the projection ${\pi }_Y$; the latter set $E\times Y$ is the pullback of the set $E$ under the projection ${\pi }_X$. Thus, $E\times F$ is the intersection of two pullback sets and is therefore contained in the product $\sigma$-algebra.

For $F$ to make ${\pi }_X:\left(X\times Y,F\right)\to \left(X,B_X\right)$ and ${\pi }_Y:\left(X\times Y,F\right)\to \left(Y,B_Y\right)$ measurable, it must at least contain the inverse image of every measurable set in $B_X$ and $B_Y$. From this, we immediate that $F$ must contain the sets of the form ${\pi }_X^{-1}(E)$ for $E\in B_X$ and ${\pi }_Y^{-1}(F)$ for $F\in B_Y$. But this is the same as saying that $F$ must contain the generating set of the product $\sigma$-algebra, which is, in turn, equivalent to saying that $F$ contains the product $\sigma$-algebra itself.

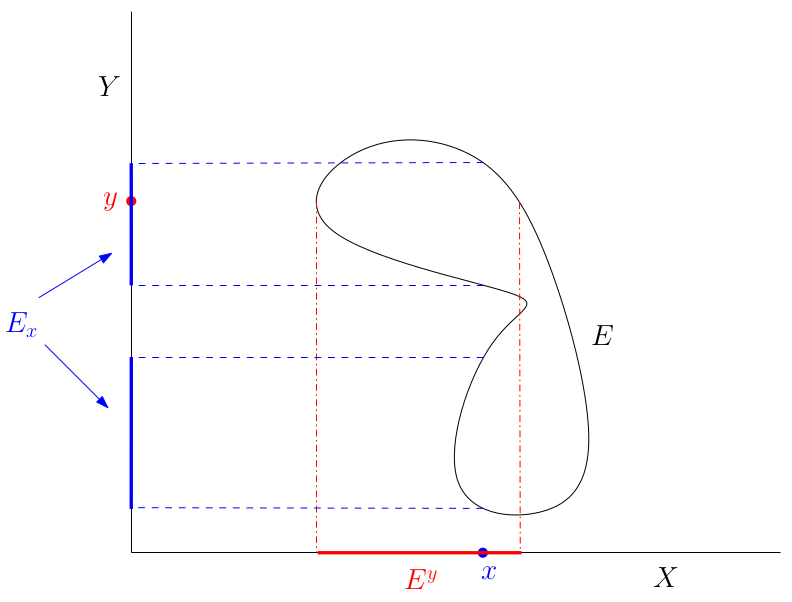
It becomes obvious that the latter form is better suited for our proof as soon as one realises that the right-hand set is a $\sigma$-algebra. Denote this set by $H$.

• We have $\varnothing \in H$ since ${\varnothing }^y={\varnothing }_x=\varnothing \in B_X,B_Y$.

• Let $E\in H$, i.e., $E_x\in B_Y$ and $E_y\in B_X$. Then,

  $${\left(E^c\right)}_x=\left\{y\in Y\mid \left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\in E^c\right\}=\left\{y\in Y\mid \left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\notin E\right\}={\left\{y\in Y\mid \left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\in E\right\}}^c={\left(E_x\right)}^c\in B_Y$$

  since $B_Y$ is itself a $\sigma$-algebra. Similarly, ${\left(E^c\right)}^y={\left(E^y\right)}^c\in B_X$.

• Let $E_1,E_2,\dots$ be a sequence of $H$-measurable sets. Using elementary set-theoretic laws, we obtain

  $${\left(\bigcup _{n=1}^{\infty }{E}_n\right)}_x=\left\{y\in Y\mid \left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\in \bigcup _{n=1}^{\infty }{E}_n\right\}=\bigcup _{n=1}^{\infty }\left\{y\in Y\mid \left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \end{array}\right]\in E_n\right\}=\bigcup _{n=1}^{\infty }{\left(E_n\right)}_x.$$

  Similarly ${\left(\bigcup <!--\; FUNCTION\; APPLICATION\; -->E_n\right)}^y={\bigcup <!--\; FUNCTION\; APPLICATION\; -->}_{n=1}^{\infty }{\left(E_n\right)}^y\in B_x.$

To demonstrate that one $\sigma$-algebra is contained in another, it suffices to demonstrate that the generating set of the former $\sigma$-algebra is contained in the second $\sigma$-algebra. We use the generating set from the part (i) of this proof, i.e., the collection $\{E\times F\mid E\in B_X,F\in B_Y\}$. An important observation that one immediately makes while playing around with sections is that

But this practically means that

Thus, $B_X\times B_Y\subseteq H$, as desired.

and similarly for ${(f^y)}^{-1}(A)={(f^{-1}(A))}^y.$