Exercise 1.10

Answers

(a)
The μ for the three coins are all 0.5 since the coins are fair. 
total_coins = 1000 
total_flips = 10 
run_once(total_coins, total_flips, True)
     Frequency of first coin: 0.5
     Frequency of a random coin: id(83)-freq(0.3)
     Frequency of the coin with minimum frequency: id(7)-freq(0.0)
     
     (0.5, 0.3, 0.0)

(b) 
total_coins = 1000 
total_flips = 10 
total_runs = 1000000 
v1s, vrands, vmins = [],[],[] 
for run in range(total_runs): 
    v1,vrand,vmin = run_once(total_coins, total_flips) 
    v1s.append(v1) 
    vrands.append(vrand) 
    vmins.append(vmin) 
 
fig, axs = plt.subplots(1,3,sharey=True, tight_layout=True) 
n_bins = 10 
axs[0].hist(v1s,bins=n_bins) 
axs[1].hist(vrands,bins=n_bins) 
axs[2].hist(vmins,bins=n_bins)
     (array([6.23941e+05, 0.00000e+00,
             0.00000e+00, 0.00000e+00,
             0.00000e+00, 3.76049e+05,
             0.00000e+00, 0.00000e+00,
             0.00000e+00, 1.00000e+01
         ]),
         array([0., 0.02,
             0.04, 0.06,
             0.08, 0.1,
             0.12, 0.14,
             0.16, 0.18,
             0.2
         ]),
      < a list of 10 Patch objects > )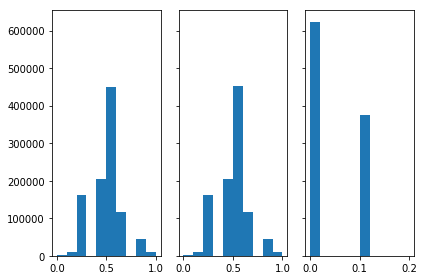

PIC
(c) 
eps = np.arange(0.0,0.5,0.05) 
bounds = hoeffding_bound(eps, total_flips) 
v1s, vrands, vmins = np.array(v1s), np.array(vrands), np.array(vmins) 
v1d = np.abs(v1s-0.5) 
vrandd = np.abs(vrands-0.5) 
vmind = np.abs(vmins-0.5) 
 
p1, prand, pmin = np.zeros(len(eps)), 
    np.zeros(len(eps)), 
    np.zeros(len(eps)) 
 
for idx in range(eps.shape[0]): 
    ep = eps[idx] 
    p1[idx] = np.sum(v1d > ep)/total_runs 
    prand[idx] = np.sum(vrandd > ep)/total_runs 
    pmin[idx] = np.sum(vmind > ep)/total_runs 
 
plt.plot(eps, bounds, 
    marker = 'o', markerfacecolor = 'blue', markersize = 8, 
    color = 'skyblue', label = 'Hoeffding Bound') 
 
plt.plot(eps, p1, 
    marker = '', color = 'r', linewidth = 1, 
    label = 'First Coin') 
 
plt.plot(eps, prand, 
    marker = '', color = 'g', linewidth = 1, linestyle = 'dashed', 
    label = 'Random Coin') 
 
plt.plot(eps, pmin, 
    marker = '', color = 'y', linewidth = 1, linestyle = 'dashed', 
    label = 'Coin with Minimum Freq') 
 
plt.legend()
     <matplotlib.legend.Legend at 0x230e84aef98>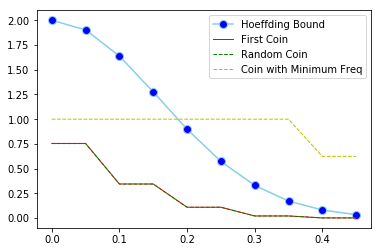

PIC
(d)
The first and random coins follow the Hoeffding bound. The coin with minimum frequency doesn’t obey Hoeffding bound. This is because for the first two coins, the coins were chosen before the experiment. While for the last one, we have to flip all the coins first and use the data to compute out which is the coin with a minimum frequency of heads. This violates the Hoeffding inequality condition which says the hypothesis h has been fixed before samples were drawn.
(e)
When we choose the coin having the minimum frequency of heads. We are like choosing the bin from 1000 bins (our hypothesis space). But we choose the bin after we finish sampling the data. This is akin to a learning algorithm for the final hypothesis. The other two coins were chosen before the sampling, which is choosing the bin beforehand.
User profile picture
2021-12-07 19:49
Comments