Exercise 3.9

1.

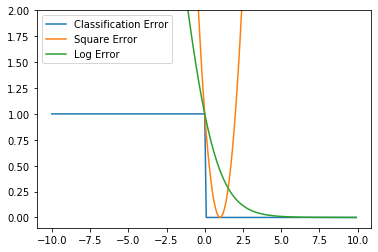
See plot below

2.

When $y=1$

• If $s\ge 0$, $e_{\mathit{class}}(s,y)=0$, $e_{\mathit{sq}}(s,y)={(1-s)}^2\ge 0$
• If $s0$, $e_{\mathit{class}}(s,y)=1$, $e_{\mathit{sq}}(s,y)={(1-s)}^2=1-2s+s^{2}1$

In both cases, we have $e_{\mathit{sq}}(s,y)\ge e_{\mathit{class}}(s,y)$. Similarly, we can prove that when $y=-1$, we have $e_{\mathit{sq}}(s,y)\ge e_{\mathit{class}}(s,y)$ as well. So $e_{\mathit{sq}}(s,y)\ge e_{\mathit{class}}(s,y)$ for all cases of $s$ and $y$. The classification is upper bounded by the squared error.

3.

When $y=1$,

(a)

If $s\ge 0$, $e_{\mathit{class}}(s,y)=0$, $e_{\mathit{log}}(s,y)=\ln <!--\; FUNCTION\; APPLICATION\; -->(1+\exp <!--\; FUNCTION\; APPLICATION\; -->(-\mathit{ys}))=\ln <!--\; FUNCTION\; APPLICATION\; -->(1+\exp <!--\; FUNCTION\; APPLICATION\; -->(-s))\ge \ln <!--\; FUNCTION\; APPLICATION\; -->1=0$, also $\ln <!--\; FUNCTION\; APPLICATION\; -->20$, so we have $\frac{1}{\ln <!--\; FUNCTION\; APPLICATION\; -->2}{e}_{\mathit{log}}(s,y)\ge 0=e_{\mathit{class}}(s,y)$.

(b)

If $s0$, $e_{\mathit{class}}(s,y)=1$, $e_{\mathit{log}}(s,y)=\ln <!--\; FUNCTION\; APPLICATION\; -->(1+\exp <!--\; FUNCTION\; APPLICATION\; -->(-\mathit{ys}))=\ln <!--\; FUNCTION\; APPLICATION\; -->(1+\exp <!--\; FUNCTION\; APPLICATION\; -->(-s))\ln <!--\; FUNCTION\; APPLICATION\; -->2$, so $\frac{1}{\ln <!--\; FUNCTION\; APPLICATION\; -->2}{e}_{\mathit{log}}(s,y)1=e_{\mathit{class}}(s,y)$

Similarly, we can prove that when $y=-1$, we have $\frac{1}{\ln <!--\; FUNCTION\; APPLICATION\; -->2}{e}_{\mathit{log}}(s,y)\ge e_{\mathit{class}}(s,y)$ as well. The logistic regression is an upper bound to the classification error.

import numpy as np 
import matplotlib.pyplot as plt 
 
def tanh(s): 
    a = np.exp(s) - np.exp(-s) 
    b = np.exp(s) + np.exp(-s) 
    return a/b 
 
def classification_error(s, y): 
    signs = np.sign(s) 
    return signs != y 
 
def square_error(s, y): 
    return (y-s)**2 
 
def log_error(s, y): 
    return np.log(1.0+np.exp(-y*s)) 
 
ss = np.arange(-10,10,0.1) 
cls_err = classification_error(ss, 1) 
sq_err = square_error(ss, 1) 
log_err = log_error(ss, 1)/np.log(2) 
plt.plot(ss, cls_err, label='Classification Error') 
plt.plot(ss, sq_err, label='Square Error') 
plt.plot(ss, log_err, label='Log Error') 
plt.ylim(-0.1, 2) 
plt.legend() 
plt.show()