Homepage › Solution manuals › Yaser Abu-Mostafa › Learning from Data › Exercise 8.6
Exercise 8.6
Answers
- (a)
-
def generate_data_84(N, x1_lb=0, x1_ub=1, x2_lb=-1, x2_ub=1): dim = 1 max_v = 10000 x1 = data.generate_random_numbers(N, dim, max_v, x1_lb, x1_ub) x2 = data.generate_random_numbers(N, dim, max_v, x2_lb, x2_ub) df = pd.DataFrame({'x1':x1.flatten(), 'x2':x2.flatten()}) df['y'] = np.sign(df['x2']) return df
N = 20 N_t = 100 df = generate_data_84(N) print(f"-- Number of positive points: {df.loc[df['y']>0]['y'].count()}") X = df[['x1', 'x2']].values y = df['y'].values my_svm = lm.SVM() my_svm.fit(X, y) print(f"-- In-Sample Error: {my_svm.calc_error(X, y)}") print(f"-- SVM Margin: {my_svm.margin()}") df_t = generate_data_84(N_t) X_t = df_t[['x1', 'x2']].values y_t = df_t['y'].values print(f"-- Out-of-Sample Error: {my_svm.calc_error(X_t, y_t)}")
-- Number of positive points: 13 -- In-Sample Error: 0.0 -- SVM Margin: 0.127515635876689 -- Out-of-Sample Error: 0.04xsp1 = df.loc[df['y']==1]['x1'].values ysp1 = df.loc[df['y']==1]['x2'].values xsm1 = df.loc[df['y']==-1]['x1'].values ysm1 = df.loc[df['y']==-1]['x2'].values #plt.tight_layout() X_train = df[['x1', 'x2']].values y_train = df['y'].values cls = my_svm x1_min, x1_max = 0, 1 x2_min, x2_max = -1, 1 xx1, xx2 = myplot.get_grid(x1_min, x1_max, x2_min, x2_max, step=0.02) myplot.plot_decision_boundaries(xx1, xx2, 2, cls) myplot.plt_plot([xsp1, xsm1], [ysp1, ysm1], 'scatter', colors = ['r', 'b'], markers = ['o', '+'], labels = ['+1', '-1'], title = "Exercise 8.6 (a) SVM", yscale = None, ylb = -1, yub = 1, ylabel = None, xlb = 0, xub = 1, xlabel = None, legends = ['+1', '-1'], legendx = None, legendy = None, marker_sizes = [5, 5])
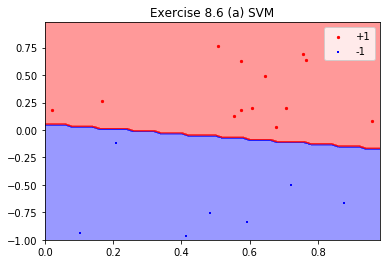
- (b)
-
df2 = pd.DataFrame({'x0':np.ones(N)}) df1 = df.copy() df1.insert(0,'x0',df2['x0']) indexes = np.arange(N) indexes[18] = 0 indexes[0] = 18 indexes[19] = 17 indexes[17] = 19 df1 = df1.reindex(indexes)
eta = 1 use_adaline=False maxit = 1000 dim = 2 positives = df1.loc[df1['y']==1] negatives = df1.loc[df1['y']==-1] figsize = plt.figaspect(1) f, ax = plt.subplots(1, 1, figsize=figsize) ps = ax.scatter(positives[['x1']].values, positives[['x2']].values, marker = '+', c = 'b', label = '+1 labels') ns = ax.scatter(negatives[['x1']].values, negatives[['x2']].values, marker = r '$-$', c = 'r', label = '-1 labels') print('Number of positive points: ', len(positives)) print('Number of negatives points: ', len(negatives)) norm_g, num_its, _ = lm.perceptron(df1.values, dim, maxit, use_adaline, eta, randomize=False, print_out = True) x1 = np.arange(0, 1, 0.02) norm_g = norm_g/norm_g[-1] c = np.ones((N_t, 1)) XX_t = np.hstack((c, X_t)) print(f"-- Out-of-Sample Error: {lm.calc_error(norm_g, XX_t, y_t)}") # ------- Ploting ------ hypothesis = ax.plot(x1, -(norm_g[0]+norm_g[1]*x1), c = 'g', label='PLA') svm = ax.plot(x1, -(my_svm.w[0]*x1+my_svm.b)/my_svm.w[1], c = 'r', label='SVM') ax.set_ylabel(r"$x_2$", fontsize=11) ax.set_xlabel(r"$x_1$", fontsize=11) ax.set_title('Exercise 8.6 (c) Data set size = %s'%N, fontsize=9) ax.axis('tight') legend_x = 2.0 legend_y = 0.5 ax.legend(['PLA', 'SVM', '+1 labels', '-1 labels', ], loc='center right', bbox_to_anchor=(legend_x, legend_y)) plt.show()
Number of positive points: 13 Number of negatives points: 7 Final correctness: 20 . Total iteration: 16 Final w: [0. 1.50015002 3.00990099] -- Out-of-Sample Error: 0.13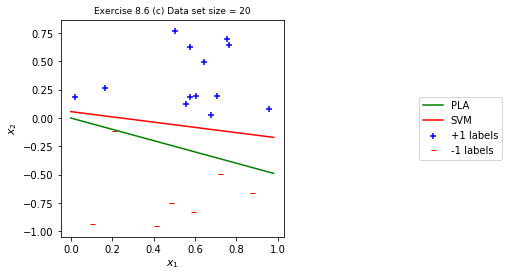
- (c)
- It’s clear that PLA can be greatly affected by the ordering of data points, while
SVM is stable with respect to the point orders.
The out-of-sample error is much larger from PLA.

2021-12-08 10:07